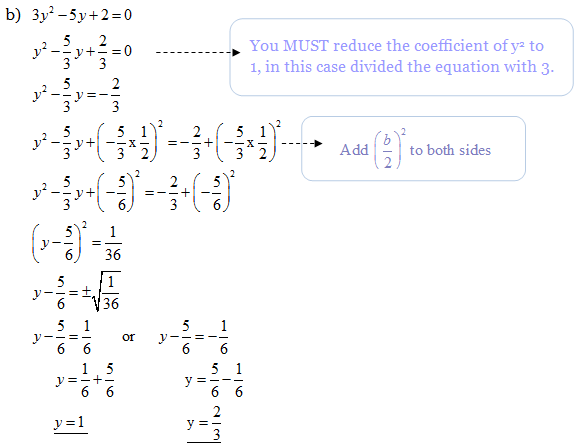Modern Mathematics Form 4: May 2015

Generally, ${{x}^{2}}-6x+5=0$ is the quadratic equation, expressed in the general form of $a{{x}^{2}}+bx+c=0$ , where a=1, b=- 6 and c=5. The root is the value of x that can solve the equations.

A quadratic equation only has two roots.

Example1: What are the roots of ${{x}^{2}}-6x+5=0$ ?
Answer: The value of 1 and 5 are the roots of the quadratic equation, because you will get zero when substitute 1 or 5 in the equation. We will further discuss on how to solve the quadratic equation and find out the roots later.

1) Solve the quadratic equations

There are many ways we can use to solve quadratic equations such as using:

1)     substitution,
2)     inspection,
3)     trial and improvement method,
4)     factorization,
5)     completing the square and
6)     Quadratic formula.

However, we will only focus on the last three methods as there are the most commonly use methods to solve a quadratic equation in the SPM questions. Let’s move on!

Factorization

Factorization is the decomposition of a number into the product of the other numbers, example, 12 could be factored into 3 x 4, 2 x 6, and 1 x 12.

Example 2: Solve ${{x}^{2}}+7x+12=0$ using factorization.
Answer: We can factor the number 12 into 4 x 3. Remember, always think of the factors which can be added up to the get the middle value (3+4 = 7), refer factorization table below,

So we will get ( x + 3 )( x + 4 ) = 0,
x + 3 = 0 or x + 4 = 0
x = – 3 or x = – 4

Example 3: Solve $10x-3=8x^2$ using factorization.
Answer: Rearrange the equation in the form of $a{{x}^{2}}+bx+c=0$

So we will get (4x – 3)(2x – 1)=0,
4x – 3 = 0 or 2x – 1 = 0
x = $\frac{3}{4}$ or x = $\frac{1}{2}$

Completing the square

Example 4: Solve the following equation by using completing the square method.

Quadratic formula

Normally when do you need to use this formula?

1)      The exam question requested to do so!
2)     The quadratic equation cannot be factorized.
3)     The figure of a, b, and c of the equation $a{{x}^{2}}+bx+c=0$ are too large and hard to factorized.

Example 5: Solve $(x-2)=6x(x+3)$ using quadratic formula.

2) Form a quadratic equation

How do you form a quadratic equation if the roots of the equation are 1 and 2? Well, we can do the work out like this using the reverse method:

We can assume:

x = 1 or x = 2
x – 1 = 0 or x – 2 = 0

(x-1)(x-2)=0
x2-2x-x+2=0
x2-3x+2=0

So the quadratic equation is x2 – 3x + 2=0. This is the most basic technique to form up a quadratic equation.

Let’s assume we have the roots of $\alpha$ and $\beta$ :

In other words, we can form up the equation using the sum of roots (SOR) and product of roots (POR). If the roots are 1 and 2,

SOR = 1+2
= 3

POR = 1 x 2
=2

${{x}^{2}}-(\text{sum of roots)}x+(\text{product of roots)}=0$

${{x}^{2}}-3x+2=0$

Sometime we need to determine the SOR and POR from a given quadratic equation in order to find a new equation from a given new roots. In general form,

Let’s look at the example below on how the concept above can help us solve the question.

Example 6: Given that $\alpha$ and $\beta$ are the roots of $5{{x}^{2}}-2x-2=0$ , form a quadratic equation $a{{x}^{2}}+bx+c=0$ with the roots of ( $\alpha$ – 5 ) and ( $\beta$ – 5 ).

3) Determine the conditions for the type of roots

Refer back to example 2, we know that ${{x}^{2}}+7x+12=0$ has two different roots (-3 and -4) by solving using factorization method. However, how are we going to determine the types of roots of ${{x}^{2}}+7x+12=0$ without solving the equation? The trick is we can use ${{b}^{2}}-4ac$ .

${{b}^{2}}-4ac$ is called a discriminant. Remember, when the value is greater than 0, we have 2 different roots, when it is 0, we have 2 equal roots, and when it is less than 0, we have no roots.

From the quadratic equation, ${{x}^{2}}+7x+12=0$ , $a=1,b=7,c=12,\text{ so }{{7}^{2}}-4(1)(12)=1$ , we have 2 different roots since the discriminant is greater than zero. Refer table below.

Example 7: A quadratic equation ${{x}^{2}}+2hx+4=x$ has two equal roots. Find the possible values of h.

Done by ; swaggy anis and lame aniyah

Chapter 4 Mathematical Reasoning

4.1 : Statements

· Determining whether a sentence is a statement
· A statement is a sentence that is either true or false but not both.

4.2 : Quantifiers "All" and "Some"

· Constructing statements using the quantifiers "all" and "some"A quantifiers denotes the number of objects or cases involved in a statement.

(a) "All" refers to each and every object or case that satisfies a certain condition.

(b) "Some" refers to several and not every object or case that satisfies a certain condition.

· Determining the truth value of statements that contain the quantifier "all" in statement that contains the quantifier "all",each and every objects is being considered in the statement.If there is one object (or more) that contradicts the statement,then the statement is false.
· Generalising statements using the quantifier "all" sometimes a statement can be generalised to cover all cases using the quantifier "all" without changing its truth value.
Constructing true statements using the quantifier "all" or "some" to construct a true statement based on given objects and their properties :

(a)Use the quantifier "all" if each and every object satisfies the given property.

(b)Use the quantifier "some" if there is one or more objects that contradicts with the given property.

4.3 Operations on Statements

· Changing the truth value of statements using the word "not" or "no"1.The word "not" or "no" can be used to change the truth value of a statement.
· The process of changing the truth value of a statement using the word "not" or "no" is known as negation.
· ~p represent the negation for statement p.

Identifying two statement from a compound statement that contains the word "and"1.In compound statement containing the word "and" we can identify two statement.
· For example,7 is an odd number and 14 is an even number.Is a compound statement that is made up from the following two statement.

® Statement 1 : 7 is an odd number.

® Statement 2 : 14 is an even number.

· Forming compound statement using the word "and"W can use the word "and" to from a compound statement from two statement.
· Identifying two statement from a compound statement that contains the word "or" In a compound statement containing the word "or" we can identify two statement.

® Statement 1 : -5 < -2

® Statement 2 :½ = 0.5

· Forming compound statements using the word "or"We can from compound statement from two statement by using the word "or"
· Truth value of compound statement that contains the word "and"1.When two statements are combined with the word "and" the compound statement formed is :

(a) True,if both statement are true.

(b) False, if one of the statement or both the statement are false.

· Truth value of a compound statement that contains the word "or"1.when two statements are combined with the word "or" the compound statement formed is :

(a) true,if one of the statement or both the statement are truth.

(b) false,if both the statement are false.

4.4 Implication

· Antecedent and consequent of an implication Statement in the form "if p,then q"is known as an implication. p is the antecedent and q is the consequent.

· Writing two implications from a compound statement containing "if and only if"A compound statement in the form "p if and only if q"is a combination of two implications.

® Implication 1 : "if p, then q"

® Implication 2 : "if q, then p"

· Constructing implications "if p,then q" and "p if and only if q"Based on the given antecedent and consequent,we can construct a mathematical statement in the form :

(a) "if p,then q"

(b) " p if and only if q"

· The converse of implicationFor the implication "if p,then q",the converse of the implication is "if q,then p".
· Truth value of the converse of an implicationThe converse of an implication is not necessarily true.

4.5 Arguments

· Premises and conclusion of an argument1. An argument consist of collection of statements,which are the premises,followed by another statement,which is the conclusion of the argument.

· Making a conclusion based on the given premisesArgument Form I

® Premise I : All A re B

® Premise II : C is A

Ø Conclusion : C is B

· For example,Premise I : All multiples of 10 has the unit digit 0

® Premise II : M is a multiple of 10

Ø Conclusion : M has the unit digit 10

4.6 Deduction and induction

· Reasoning by deduction and induction1.Deduction is the process of making a specific conclusion based on a general statement.
· Induction is the process of making a general conclusion based on specific cases.
· Making conclusion by deductionThrough reasoning by deduction ,we can make conclusion for a specific case based on a general statement.
· Making generalisations by induction.Through reasoning by induction,we can make generalisation based on the pattern of a numerical sequence.

Credit: http://allspmnotes.blogspot.com/2012/12/mathematics-notes-form-4-all-topic.html

Modern Mathematics Form 4

Thursday 7 May 2015

Chapter 2 Quadratic Expressions and Equations